Angle explains: automated market makers

https://blog.angle.money/angle-explains-amms-22daddf51f32

Angle, Jul 2022

Recent research showed that most of us are losing money when providing liquidity to Uniswap V3. How come ? Probably because Automated Marker Makers are complex objects. But it’s worth digging into: besides being the most used DeFi protocols, they are also an interesting and beautiful mathematical concept.

AMM stands for “Automated Market Maker”. It’s basically a smart contract that manages liquidity provided by Liquidity Providers to create an on-chain marketplace. We use them every time we do on-chain swaps.

The most known AMMs (Uniswap and its forks, Curve, Balancer) respect certain properties:

• They do not need any human input and are described by mathematical invariants, which dictates what swaps they authorize. The most known of is Uniswap V2’s invariant x*y = k. The smart contract holds x token X and y token Y, and allows any swap dx for dy that preserve the invariant. So any swap such that (x+dx)*(y-dy) = k.

• In addition to being driven by a mathematical formula, they are “path independent”, meaning that if we don’t account for accrued fees, their states only depend on the prices. So as a LP, if you add liquidity and remove it at the same price, you can’t have made a loss.

Let’s do a step-by-step example to better understand. Assume you have 1000€ to invest on the agEUR / ETH pair, and that the starting price of ETH is 1000€. If you do nothing and hold only one of the 2 assets, your returns in € after a year would be:

Holding agEUR versus holding ETH

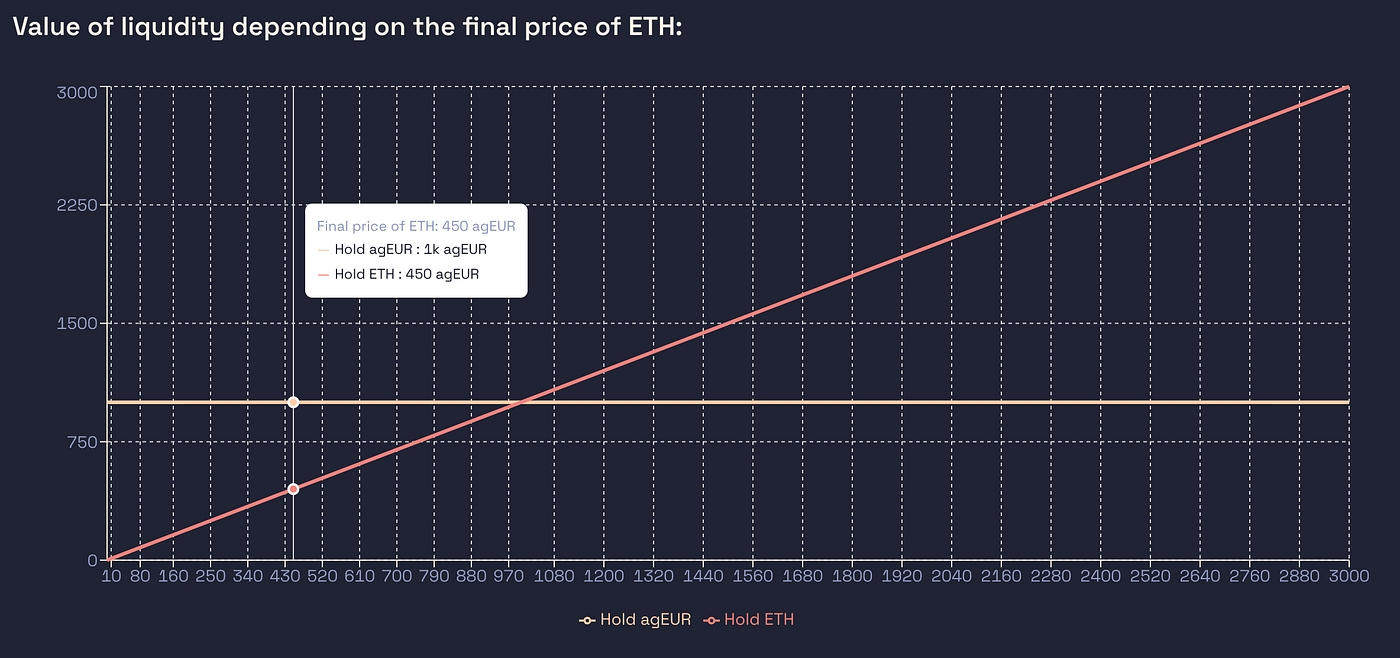
It may seem complex, but this graph basically says that you’ll have 1000€ if you’ve held agEUR or whatever 1 ETH will be worth a year from now if you’ve held ETH.

Now assume you want to provide liquidity in Uniswap V2. You’ll have to bring 500 agEUR and 0.5 ETH at first. Would it be better than holding those 500 agEUR and 0.5 ETH ? Without taking fees accrued by the AMM into account, after a year you’ll have:

Uni V2 LP without fees versus holding 50% agEUR / 50% ETH

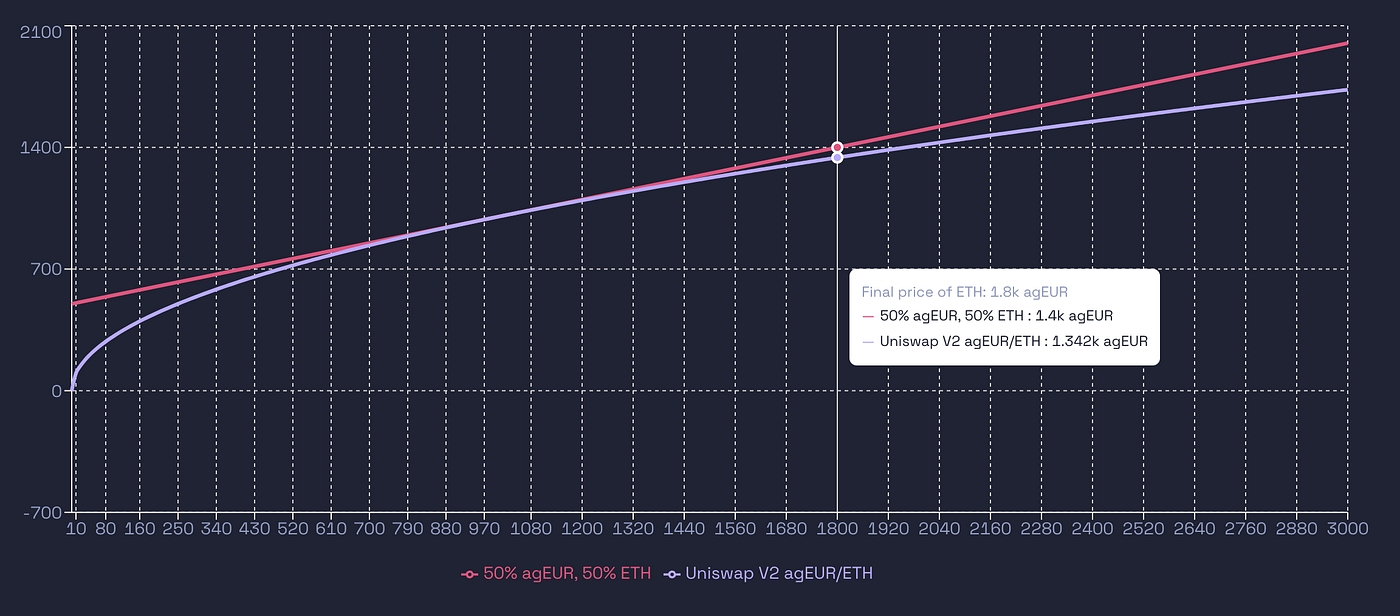
See the difference between the red curve and the purple curve? This is the infamous Impermanent Loss a.k.a. “IL”, that is to say what you’ve lost by enabling others to swap your assets.

There are numerous proposals out there of protocols or magical techniques to “eradicate” IL, but it is somehow inherent to AMMs: if you allow traders to swap your liquidity, then you’ll be left with a different asset balance than what you brought, which may be worst than having let them idle in the first place. So how do LPs earn ? Thanks to fees and the “path independent” property: with a reasonable price change, after some time the pool will be back to a state close to its original one and will have accrue some fees.

Let’s add add these fees to the previous curve. Let’s assume the volume is 100 agEUR / days for a year and the pool has a 0.25% fee. The graph would then be:

Uni V2 LP versus holding 50% agEUR / 50% ETH

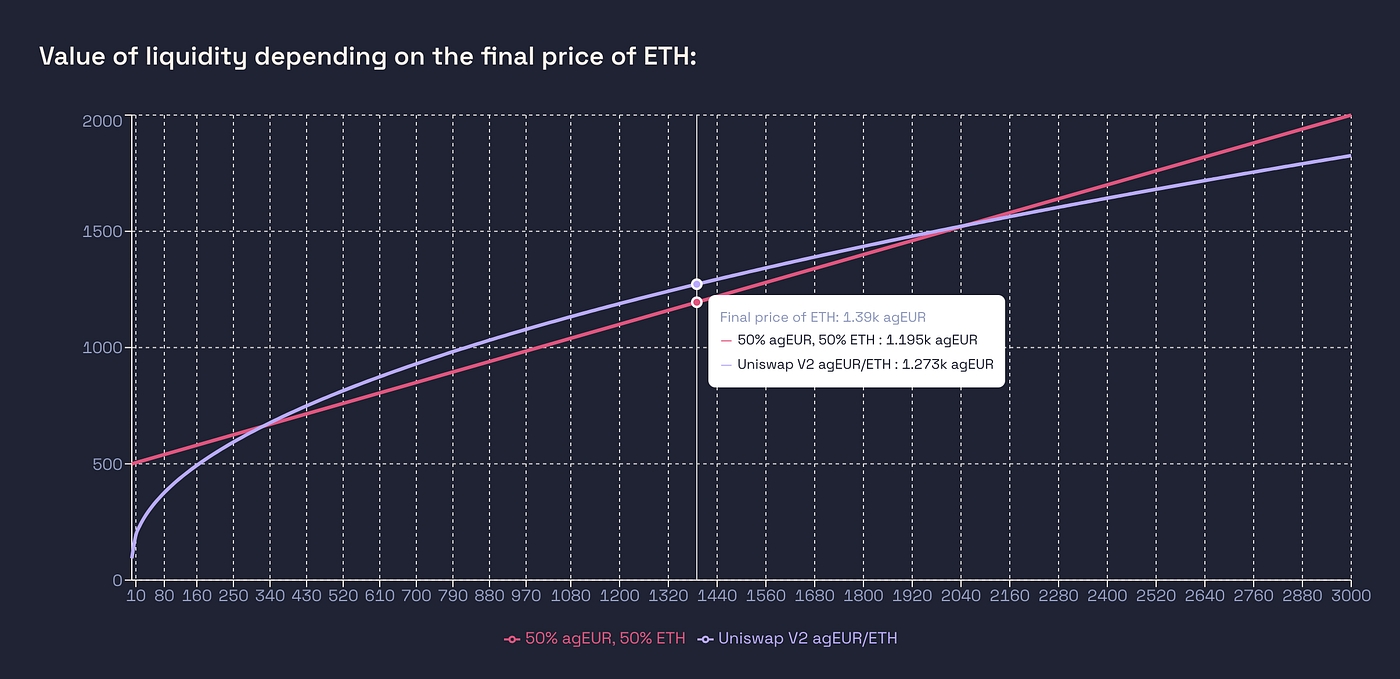
Now we see all the potential benefits of LPing: in this scenario, without price change, there would be a ~9% APR !

Let’s now deal with Uniswap V3. Briefly, it’s is a complexification of Uniswap V2: the mathematical invariant is the same, but LPs can “concentrate” their liquidity on a price range by adding a “virtual” liquidity to the pool. Let’s not dig into the maths this time but focus on what the implications for LPs are.

When adding liquidity on Uniswap V3, you choose a price range, which defines the amount of “virtual” liquidity you’re also adding to the pool. The more your range is small, the more “virtual” liquidity you add to the pool, which’d mean more IL but bigger swaps so higher fees to move the pool price.

In the extreme case of a range 0-infinity, you’re back in the Uni-V2 case. Let’s take the example of a 500–2000 range and compare Uniswap V3, V2 and holding:

Uni V2 LP versus Uni V3 LP versus holding 50% agEUR / 50% ETH, without fees

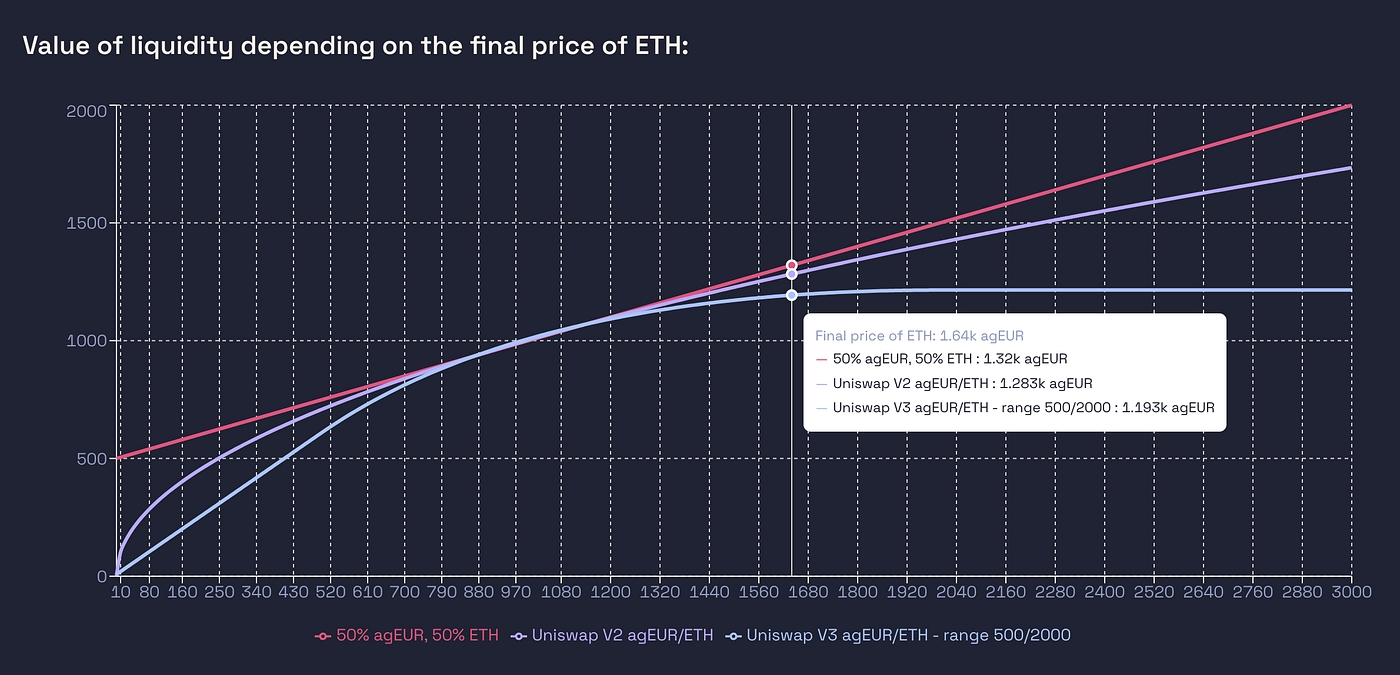
What happens ? When the price reaches 500, everything has been swapped to ETH so the Uniswap V3 position only contains ETH, and when it reaches 2000, there is only agEUR left in the position. The IL is much stronger that Uniswap V2. But it also means that to move the price of the AMM, more liquidity needs to be swapped, so there will be more arbitrages and more fees earned by LPs. But how much ?

For the purpose of this simulation, we can therefore 2 types of volumes:

• a daily “intrinsic” volume: all the swaps that are not an arbitrage, and that are not made in order to move the price of the pool. It includes for example all the retail, spot orders. This volume will not be higher depending on the AMM type.

• a volume due to arbitrages between market places, that aims to move the price of the pool. This one can be estimated given a daily price change and the formula of the AMM: you can compute the swap size needed to move the pool price, hence the fees earned.

Let’s assume a mean price deviation of 10%, implying more volume and fees for the UniV3 pool:

Uni V2 LP versus Uni V3 LP versus holding 50% agEUR / 50% ETH

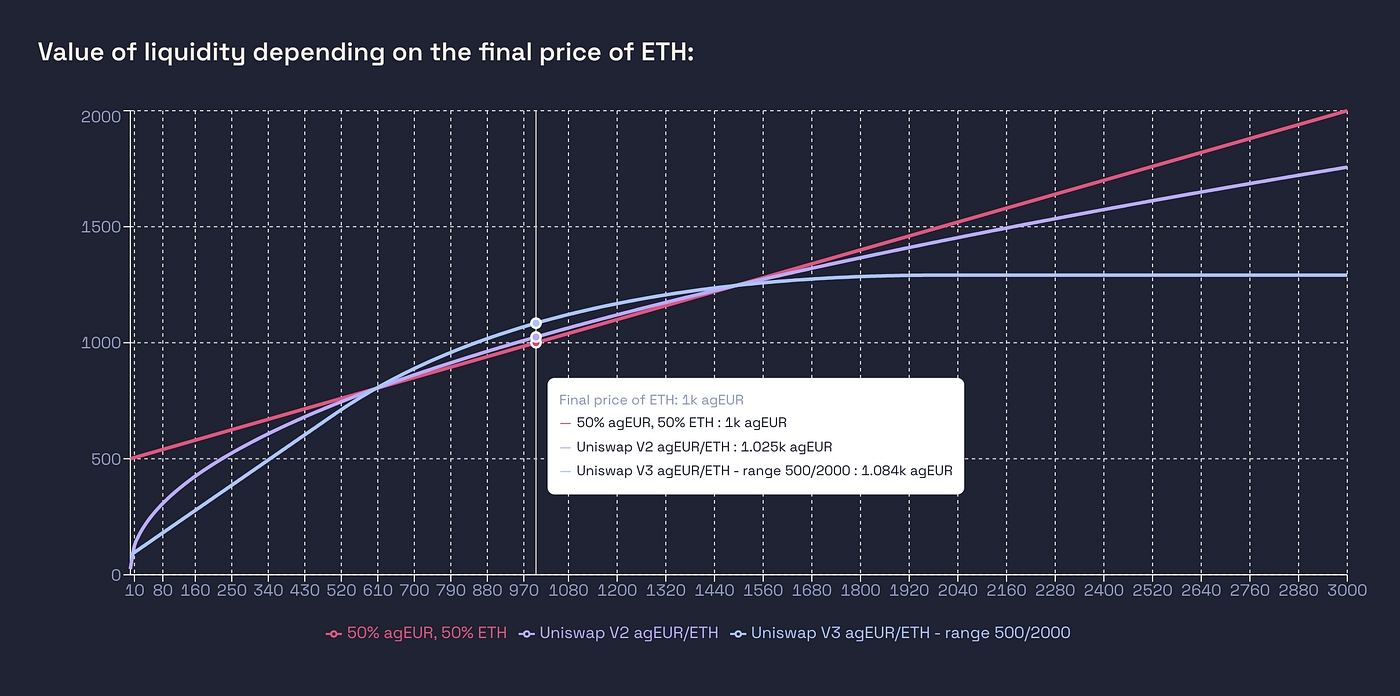
In this scenario, the Uni V3 liquidity was able to generate more arbitrages, leading to more fees and hence more revenue for LPs, but at the cost of a more important IL in most cases. Basically for the same price deviation more of your liquidity will be swapped, which generates more fees but also more IL: check for yourself using https://app.angle.money/#/amm.

Another cool feature of Uni V3 is that by adding multiple LP positions, or choosing your range carefully, you can reproduce any type of market. Let’s do just one example: starting at 1 ETH = 1000 agEUR, this is what you’ll get when providing liquidity on the range 1450–1550 versus going all in ETH and taking profits at 1500.

Uni V3 versus holding ETH until 1500, then holding agEUR

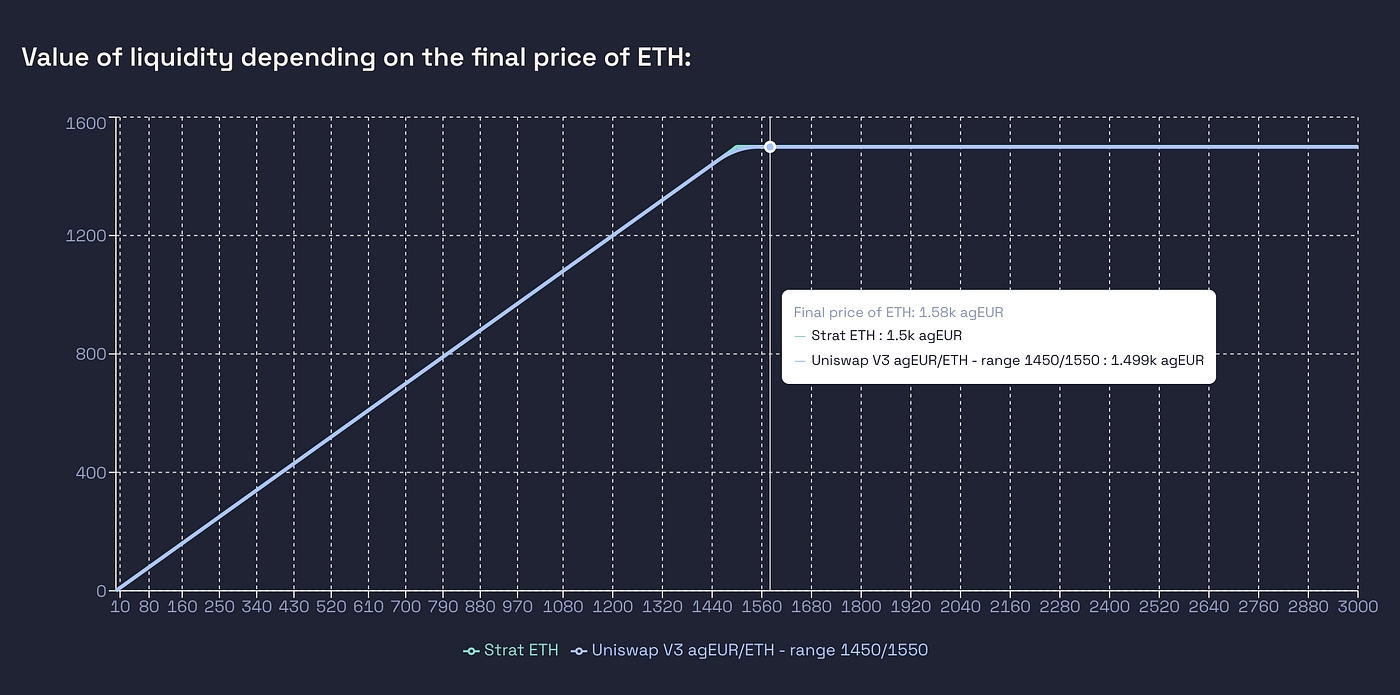
I hope this first article has helped to make AMMs clearer. Feel free to reach out and to play with our simulation tool that we use internally for decision-making !